Nimiq Validator Trustscore ​

The Validator Trustscore (VTS) helps users assess the reliability of validators in the Nimiq Wallet. This score ranges from 0 to 1, where 0 indicates a validator is not trustworthy, and 1 indicates a highly trustworthy validator. The VTS enables stakers to make informed decisions when selecting validators.

The VTS score is calculated using three key factors:

• Dominance: Ensures no validator has excessive influence by penalizing validators with a higher share of the total network stake.
• Reliability: Measures how consistently a validator produces blocks over the past nine months.
• Availability: Assesses how often a validator is online and actively selected to produce blocks.

The algorithm is designed to promote decentralization, fairness, and consistent network participation. Below is an example of how the VTS might appear in the Nimiq Wallet:

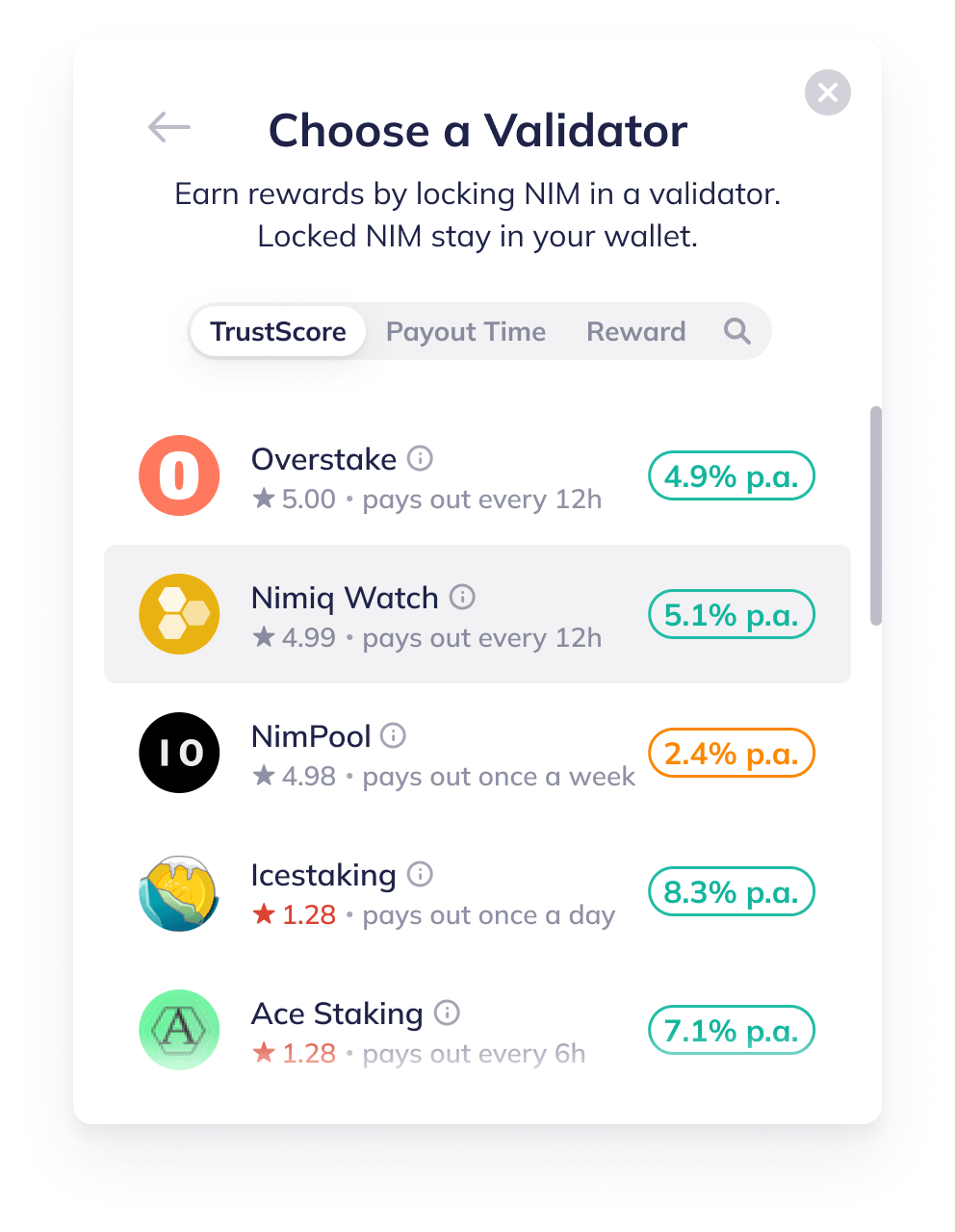
The VTS Technical Breakdown ​

The VTS algorithm uses three factors: Dominance, Reliability, and Availability. Each factor is calculated independently, with values ranging from 0 to 1, and their calculation determines the final score.

The dominance factor is based on the dominance of the validator's stake relative to the total stake in the network. Reliability and availability are based on behavior over the last nine months. For these parameters, only completed epochs are considered, not the currently active one. Therefore, the score is not live and can have a delay of up to 12 hours (an epoch lasts 12 hours).

Calculation of $m$ ​

Because reliability and availability are based on the behavior of validators over the last 9 months, we need to define 𝑚 the number of epochs to consider within this timeframe. This value ensures that all calculations include only completed epochs for accuracy. Where:

Block duration and blocks per epoch are constants defined in the policy.

Dominance ​

The dominance factor ensures that no single validator controls an excessive portion of the network's total stake. Validators with a larger stake receive a lower score to encourage a fairer distribution of control across the network. This approach penalizes disproportionately large stakes while promoting diversity in validator participation.

Dominance Ratio ​

The dominance ratio ($s$) of a validator is calculated using one of two methods, depending on the epoch's state. However, due to technical limitations, only the Active Epoch Method is currently implemented and used.

Active Epoch Method: During an active epoch, the dominance ratio is determined by dividing the validator's share by the total network share:

Where:

• $v$: The validator's share.
• $Z$: The total network share.

This method relies on the getActiveValidators function from the RPC, which provides real-time balances of each active validator.

Finished Epoch Method: For a closed epoch, a less precise fallback method exists, but is not currently implemented. This approach calculates the dominance ratio based on slot distribution across voting blocks. The ratio is derived by dividing the number of slots allocated to a validator by the total slots in the epoch:

Where:

• $sl$: The number of slots allocated to the validator.
• $Sl$: The total number of slots in the epoch.

While this method is defined in the code as dominanceRatioViaSlots, it is not actively used in practice.

Curve adjustment ​

After determining the dominance ratio, a curve is applied to calculate the dominance score $S$:

Where:

• $t=0.15$ is the threshold.
• $k=7.5$ is the slope of the curve.

The following table illustrates how the dominance score varies with the stake percentage:

Reliability ​

The Reliability factor measures how consistently a validator produces blocks when expected. Validators who reliably produce their assigned blocks will have a high score, while those who fail frequently will receive a lower score. The reliability score is calculated as a weighted moving average over multiple epochs, emphasizing recent performance.

Calculating Reliability for an Epoch ​

The reliability score for a single epoch $r_i$ is calculated as:

Where:

• $C_i$: The number of blocks produced by the validator in epoch $i$ that received rewards.
• $H_i$: The expected number of blocks the validator was likely to produce in epoch $i$.

Calculating $C_i$ ​

$C_i$ represents the total blocks rewarded to the validator in epoch $i$:

Where:

• $c_j$: The number of blocks produced by the validator in batch $j$ of epoch $i$.
• $N$: The total number of batches in the epoch (retrievable from the policy). The number of blocks a validator produced can be retrieved from the blockchain via the rewarded inherent of each batch.

Calculating $H_i$ ​

$H_i$ represents the expected likelihood of the validator producing blocks in epoch $i$:

Where:

• $h_{i,v}$: The total slots assigned to the validator $v$ in epoch $i$.
• $V$: The total number of active validators in epoch $i$.

Combining Reliability Scores Across Epochs ​

To calculate a validator's overall reliability score, we use a weighted moving average of scores across multiple epochs. More recent epochs are given higher weight:

Where:

• $m$: Total number of epochs considered.
• $a$ = 0.5: Parameter determining how much weight the oldest epoch receives compared to the newest epoch, helping to balance the influence of recent versus older performance tendencies in the weighted moving average.

Adjusting for High-Reliability Expectations ​

The formula for the weighted moving average $\overline{R}$ provides a baseline reliability score. However, to better reflect the high standards expected of validators, an additional adjustment is applied. This adjustment penalizes validators with lower reliability more severely, emphasizing the importance of consistent performance.

The adjusted reliability score $R$ is calculated using the following formula:

Where:

• $c=-0.16$: Defines the slope of the arc and determines the position of the curve. The adjustment formula is based on a circular arc, with the center of the circle at $(c,-c+1)$.

This adjustment maps the reliability score to a curve, making penalties for lower scores sharper while preserving high scores for reliable validators.

For example, a baseline reliability score of $\overline{R}=0.9$ may correspond approximately to 10% downtime, reflecting significant but not catastrophic validator underperformance. Validators with lower scores experience increasingly steep penalties, ensuring that unreliable validators are disincentivized.

Note that using 10% is only a heavy approximation. The value of 0.9 could represent 10% downtime, but also 20% or 5%, depending on when the downtime occurred. We use 10% to provide a relatable scale for the reader.

Availability ​

The availability factor measures how often a validator is online and selected to produce blocks. Validators that are consistently selected and actively producing blocks receive a higher score, promoting reliable participation and network security.

Why Availability Matters ​

Without availability, a validator could have high dominance and reliability scores but still not actively contribute to the network. This would misrepresent their role in maintaining the network's operation. The availability factor ensures that only validators selected to produce blocks are evaluated, penalizing those that fail to participate effectively, whether due to inactivity, being jailed, or missing blocks when offline.

In this context, we cannot measure how long a validator is online but can only determine when they are selected to produce blocks. A validator may be considered active yet fail to produce blocks. Availability focuses on participation in block production, regardless of online or offline status. For instance:

• A validator might not produce blocks because it hasn’t been selected in a specific period.
• In the other hand, a validator may be offline, causing it to miss block production when selected.

Availability reflects how often a validator is selected to produce blocks, regardless of their online status.

How to Calculate Availability ​

The availability score for a single epoch $l_i$ is calculated as follows:

Where:

• $l_0$: The availability score for the most recent epoch.
• $l_{m-1}$: The availability score for the oldest epoch.

To combine availability scores across epochs into a single value, we calculate a weighted moving average, where more recent epochs have higher weights:

Where:

• $m$: Total number of epochs considered.
• $a=0.5$: Determines the relative weight of the oldest epoch compared to the most recent one.

Adaptation to support smaller validators ​

To support smaller validators in our PoS network, an adjustment curve is applied to the moving average. This reduces penalties for validators that are less frequently selected for block production, while still incentivizing active participation. This adjustment ensures fairness for smaller validators, encouraging them to stay active while maintaining accountability for all participants.

The adjusted availability score $L$ is calculated as:

Suggestions & Feedback ​

Like everything in Nimiq, this algorithm is designed with the people in mind. We always welcome feedback and suggestions to make it even better. If you’d like to share your thoughts, feel free to open an issue or join our Telegram group.